Distribuciones
Empleadas Para Estimar La Mantenibilidad.
Al igual que para la
confiabilidad, la mantenibilidad también es estimada mediante la aproximación
de los respectivos datos a modelos específicos, entre los cuales, los más
empleados son:
· Distribución exponencial: Se adapta muy bien
cuando las intervenciones al equipo son de corta duración, que constituyen
principalmente intercambio de piezas estándar, su expresión matemática, es una
ecuación exponencial negativa como se muestra a continuación:
M(t): es la función mantenibilidad, que representa la
probabilidad de que la reparación comience en el tiempo
t= 0 :y sea concluida satisfactoriamente en el tiempo t
(probabilidad de duración de la reparación).
e: constante Neperiana (e=2.303..)
µ: Tasa de reparaciones o número total de reparaciones
efectuadas con relación al total de horas de reparación del equipo.
t: tiempo previsto de reparación TMPR
·
Distribución de Gumbell: Esta es la
distribución más comúnmente empleada para estimar la mantenibilidad, debido a
que puede ser aplicada cuando se tienen intervenciones cortas y algunas largas,
pero principalmente porque los cálculos son muy sencillos, debido a la
existencia de un papel funcional que simplifica la metodología de evaluación
del índice.
La ecuación que representa esta
distribución es como sigue:
Donde:
P(t)= Densidad de probabilidad.
a= Parámetro de dispersión.
t= Tiempo en estudio (TPFS).
m= Parámetro de
posición.
Los parámetros anteriores, pueden ser
encontrados de una manera sencilla utilizando el papel probabilístico, también
llamado papel de tipo gumbell.
El parámetro de dispersión “a”, se
calcula mediante la expresión:
Donde:
= 1 Y Tiempo fuera de
servicio para P(t)= 27%.
= 2 Y Tiempo fuera de
servicio para P(t)= 95%.
El parámetro de posición “m”, corresponde al TFS
para una probabilidad defalla de 36.8%
Referencia:
Rodriguez. M, (2014, 20 de Abril) Estudio
del mantenimiento de los equipos críticos De un sistema de deshidratación de
gas natural. (1998).[saber.ucv.ve] de:
http://saber.ucv.ve/jspui/bitstream/123456789/224/1/Tesis.PDF
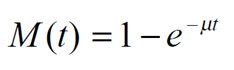



No hay comentarios:
Publicar un comentario